Ris-k

I have been playing a lot of Risk with my family recently and got to wondering what the chances of success are per battle. The internet says the following:

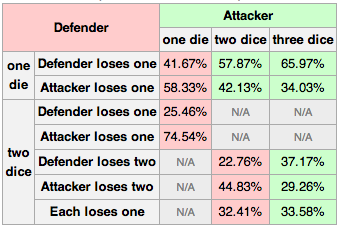
What might it look like to generate these results on our own using simulated dice throws and battles? Because this is one of those toy problems that is quite math-y, let's use k, or kona to be precise. It will allow us to be terse almost to the point of having executable formulae that define our problem.

Let's generate 50,000 simulated roles of three attackers vs two defenders, if the internet is correct we should see something close to 37% for the attacker winning both, 33% for going one-and-one and a 29% chance of the attacker losing both soldiers. Here is the code we can use to do that:

 n:50000.
 r1:{1+1 _draw 6}; r2:{a@>a:1+2 _draw 6}; r3:{2#a@>a:1+3 _draw 6}
 {(#x)%n}'={a@>a:+/'x}(r3'!n){0<x-y}'r2'!n

 / the result I got this run  => 0.37436 0.3346 0.29104

Looks like the internet never lies, our results are within a few tenths of a percent across the board with 37.4% attacker wins both, about 33.5% of going one-and-one and 29.1% of the attacker losing both soldiers.

I won't go over the "how" in terms of the code too deeply, but briefly, this is what each line says (for more on the syntax, some good resources are the k reference manual, the kona wiki and Programming in k)

n:50000. defines the number of runs as a floating point number.

r1:{1+1 _draw 6}; ... r3:... defines the functions roll 1, roll 2 and roll 3 as returning a list of sorted integers that represent the each of the dice thrown per player. Because at most the defender can only engage two soldiers, the roll 3 function takes the 2 highest for the fight and is only ever called by the attacker.

{(#x)%n}'={a@>a:+/'x}(r3'!n){0<x-y}'r2'!n in words would read (from left to right) as "return the percent of the total (#x)%n for each group x generated by grouping = the sorted list a@> that was generated summing over each sub list a:+/'x generated by applying the function 0<x-y to the lists representing n rolls of the attacking dice (r3'!n) and n rolls of the defending dice r2'!n."

As I was looking up the percentages, I came across an interesting article that simulated repeated battles given a starting number of troops per side, not just chances per discrete battle. Let's model that as well. Using the roll functions from above.

 r:(r3;r2;r1)                   / rolls 
 gr:{(r@*&(x+1)>3 2 1)[]}       / get roll type by number of soldiers
 c:{0<((#b)#gr x)-b:gr x&2&y}   / get result of single battle by num attack, defend 
 b:{{{&/(x;y)}. x}{{(x-+/0=a;y-+/1=a:c[x;y])}. x}\(x;y)}    / battle!
 
 b[40;40]
 / the result I got this run (attacker in first column, losing here) => 
 (40 40
 39 39
 37 39
 35 39
  ... 
 4 4
 4 2
 2 2
 0 2)

To be able to battle we need to account for the different combinations that can arise as the troops on each side dwindle. We do that with the function c which takes the minimum of 2 (the max for a defender), the number of defenders and the number attacking x&2&y, gets a roll and lines it up with the the number attacking ((#b)#gr x) (3v2, 3v1, 2v2, 2v1, 1v1) returning the results as a list of losses for the defender. We do this iteratively, applying the wins and losses to each army (x-+/0=a;y-+/1=a:c[x;y]) until one side is exhausted {&/(x;y)}.

If we want to run a number of battles, here keeping each side at starting with 15, we can do that with the following. We will run 10 battles, here we see the attacker in the first column winning 7/10:

{*|b[15;15]}'!10
(11 0
 0 3
 4 0
 9 0
 2 0
 0 2
 5 0
 0 2
 6 0
 4 0)

None of these simulations seemed to have helped me too much though, I lost again tonight :)